Зубчатые передачи как одни из основных элементов конструкции различных механизмов и машин известны с древних времен, а теория зацеплений является одним из фундаментальных прикладных разделов физико-математической науки и общего машиностроения.
Современный этап развития теории и практики зацеплений, основанный на использовании инновационных компьютерных технологий и трехмерного моделирования, позволяет решать новые задачи, в том числе при разработке нетрадиционных типов зубчатых зацеплений с оптимизированными геометрическими параметрами зубьев.
К настоящему времени широкое промышленное применение получили три основных типа цилиндрических зубчатых передач внешнего и внутреннего зацепления, отличающиеся профилем зубьев и технологией их изготовления [1]:
— эвольвентные;
— циклоидальные (включая цевочные);
— с круговыми зубьями (Новикова).
Среди всего многообразия зубчатых передач с технологической точки зрения можно выделить эвольвентные и циклоидальные передачи, торцовый профиль колес которых образуется методом обкатки зубчатой рейки по основной окружности. Профилирование от зубчатой рейки является наиболее общим и универсальным способом построения профиля зубьев, а в случае смещения рейки относительно основной окружности это позволяет проводить корригирование формы зубьев, добиваясь оптимальных показателей зацепления для различных эксплуатационных условий.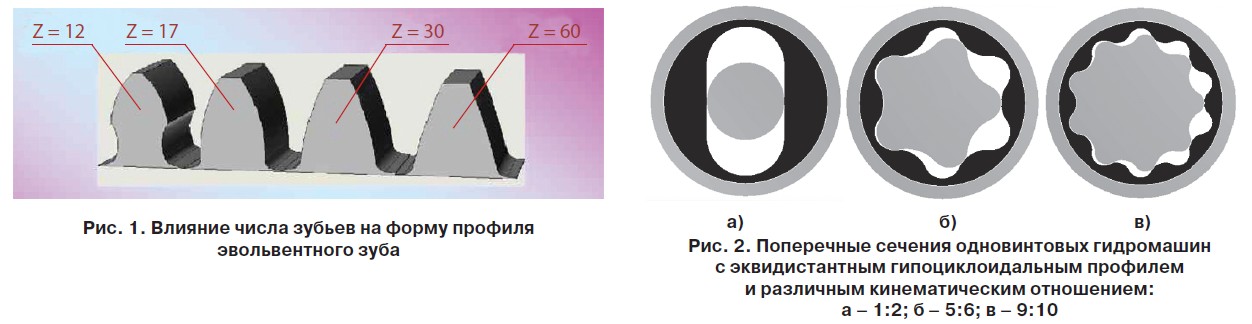
Колеса с эвольвентным профилем зубьев — наиболее распространенные в машиностроении — имеют значимые технологические и эксплуатационные преимущества по сравнению с другими типами зацеплений [2]: простой инструмент для нарезания зубьев; постоянное положение общей нормали к профилям сопряженных зубьев, что снижает динамические нагрузки; нечувствительность к небольшому изменению межосевого расстояния.
Эвольвентное зацепление в настоящее время является основой при разработке большинства передаточных устройств для механизмов и машин всех отраслей промышленности и сельского хозяйства, а теория наиболее полно разработана применительно к этому типу зацепления [1].
Классический эвольвентный профиль зубьев колес механических передач и рабочих органов объемных насосов образуется как огибающая исходного контура зубчатой рейки, представляющей собой равнобедренную трапецию с углом 20° и смещенную в общем случае относительно производящей прямой и основной окружности[3]. В настоящее время подавляющее большинство отечественных зубчатых цилиндрических колес различного назначения имеют профиль боковых граней зубьев, построенный на базе стандартного (некорригированного или корригированного за счет смещения рейки) или частично модифицированного (например, с асимметричным профилем, продольной коррекцией зубьев с целью повышения нагрузочной способности передачи) эвольвентного зацепления.
Вместе с тем, несмотря на большое число положительных эксплуатационных и технологических качеств эвольвентных профилей зубьев, одним из существенных их недостатков является склонность к подрезам и самопересечениям при малых числах зубьев колес (как известно, для эвольвентного профиля без смещения zmin=17, рис. 1), что снижает эффективность и область применения эвольвентных зубчатых передач, увеличивает их массогабаритные и стоимостные показатели, а также ограничивает возможности при проектировании рабочих органов роторных машин. Кроме того, выпуклый контакт поверхностей в случае внешнего зацепления колес увеличивает контактные напряжения и снижает несущую способность передачи.
Колеса с циклоидальным профилем характеризуются плавностью контура, возможностью реализации зацеплений с минимальным числом зубьев (включая одно- и двухзаходные) без опасности подрезания профиля и возможностью создания передач внутреннего зацепления колес с числами зубьев, отличающихся на единицу (что используется в планетарных редукторах и рабочих органах роторных гидравлических машин, компрессоров и ДВС).
Циклоидальный профиль обладает наиболее широким диапазоном изменения формы зубьев, что позволяет разрабатывать механические передачи практически с любым необходимым сочетанием чисел зубьев и кривизны сопряженных колес. При использовании циклоидального зацепления появляется возможность создания малозубых профилей одного знака кривизны (круглого, овального, треугольного с криволинейными гранями), что требуется для разработки высокоэффективных роторных машин.
Исходный циклоидальный профиль, относящийся к наружному или внутреннему элементу зубчатой пары, образуется от укороченных гипо- и эпициклоид; их эквидистант; а также как огибающая циклоидальной рейки [4].
Внецентроидный профиль, образованный от укороченной циклоидальной кривой (когда производящая точка расположена не на катящейся окружности), получил наибольшее распространение в машиностроении.
Эквидистантный профиль, для которого характерны плавность контура и непрерывное изменение положения контактной точки на сопряженных поверхностях статора и ротора (сочетание скольжения и качения), нашел повсеместное применение в рабочих органах одновинтовых насосов и гидродвигателей [5] (рис. 2).
По соотношению чисел зубьев (заходов) различают циклоидальные механизмы с произвольными числами зубьев колес и с числами зубьев, отличающихся на единицу.
Вариант z1–z2=1 для внутреннего зацепления применяется в двух случаях:
1) в планетарных редукторах, что обеспечивает получение максимального передаточного отношения и распределение нагрузки одновременно по нескольким парам сопряженных зубьев колес;
2) в рабочих органах роторных объемных машин с целью образования изолированных рабочих камер, герметично отделенных от входа и выхода.
По расположению профилей с внутренним зацеплением, числа зубьев которых отличаются на единицу, могут применяться схемы, в которых колесо с меньшим числом зубьев является внутренним или наружным элементом.
Выбор варианта одной из этих схем при заданном исходном профиле (эпи- или гипо-) определяется конструктивными требованиями проектируемой машины и зависит от способа построения сопряженного профиля (как внутренней или внешней огибающей) и соотношения радиусов начальных окружностей (центроид) исходного и сопряженного профилей.
Вариант, когда большее число зубьев приходится на профиль статора, характерен для рабочих органов винтовых насосов (кинематическое отношение 1:2) и гидромоторов (3:4…9:10) с эквидистантным зацеплением (рис. 2), в то время как вариант, при котором статор имеет на единицу меньшее число зубьев, чем находящийся внутри него ротор, относится к известным схемам двигателей внутреннего сгорания и компрессоров с внецентроидным неэквидистантным зацеплением и кинематическим отношением 3:2 и 2:1 (рис. 3).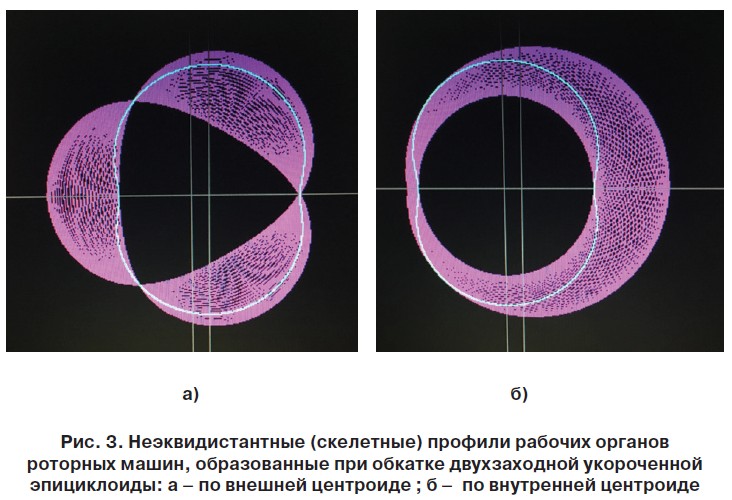 
По относительному движению сопряженных циклоидальных профилей зубьев различают механизмы: с переменными условиями касания (когда точка контакта перемещается как по исходному, так и сопряженному профилю), с частично переменными условиями касания только по одному из профилей (например, по статору), в то время как сопряженный профиль находится в зацеплении в одной неизменной точке.
Переменные условия касания профилей характерны для зацепления эквидистантных циклоидальных механизмов (когда обе скорости качения по сопряженным профилям не равняются нулю). Постоянные условия касания одного из профилей относятся к случаю зацепления профилей, образованных непосредственно от гипо- или эпициклоид без процедур их эквидистантирования.
При условии постоянного касания одного из профилей представляется возможность создать в механизме подвижный (на точке профиля внутреннего элемента) или неподвижный (на точке профиля наружного элемента) локальный узел уплотнения, расположив его в зависимости от схемы механизма, соответственно, на поверхности ротора или статора.
Примерами циклоидальных механизмов с постоянными условиями касания одного из профилей (рис. 3) являются роторнопоршневой двигатель Ванкеля и роторный компрессор (постоянный контакт вершин выступов зубьев ротора), а также газовый двигатель с постоянным контактом вершин выступов зубьев трехзаходного статора.
Основное применение циклоидального профиля в нефтегазовой отрасли — одновинтовые гидравлические машины с эластичной обкладкой статора [5], рабочим органом которых является винтовой героторный механизм с внутренним эквидистантным циклоидальным зацеплением (рис. 2).
Для многозаходных винтовых героторных механизмов (z2 ≥ 2) сопряженные торцовые профили винтовых поверхностей статора и ротора образуются по методу обкатки циклоидальной рейки, исходный контур которой предложен инженерами Пермского филиала ВНИИБТ [4, 6]. В общем случае при заданном контурном диаметре героторного механизма форма циклоидального профиля определяется сочетанием пяти безразмерных геометрических параметров (передаточного отношения, коэффициентов типа зацепления (эпи- или гипо-), внецентроидности, формы зуба и смещения рейки), что усложняет технологию изготовления (вследствие необходимости выполнения процедуры эквидистантирования контура рейки) и выбор оптимальной формы профилей, описываемых сложными математическими выражениями, зависящими от сочетания пяти вышеуказанных безразмерных параметров.
Внешнее циклоидальное зацепление может быть использовано в механических передачах и рабочих органах насосов и компрессоров, поскольку позволяет получать большое передаточное отношение в одной ступени в связи с отсутствием ограничений по числу зубьев вплоть до использования однозубой шестерни (поперечное сечение которой представляет собой окружность со смещенным центром как в классической и апробированной на практике схеме насоса Муано, рис. 2а). В этой связи отметим, что разработанное в последние годы томскими инженерами так называемое эксцентриково-циклоидальное зацепление не следует относить к отдельному типу зацепления, так как оно является предельным частным случаем внешнего циклоидального зацепления, геометрия которого известна из литературных источников и патентного фонда [5, 7].
Циклоидальное зацепление в различных нефтепромысловых механизмах (цилиндрические передачи буровых лебедок и насосов, систем верхнего привода буровых установок и штанговых винтовых насосов, станков-качалок; реечные подъемники; планетарные передачи) в перспективе может обеспечить следующие эксплуатационные преимущества: пониженное число зубьев ведущей шестерни (z=1–6) и, как следствие, минимальные массогабаритные показатели и повышенные передаточные отношения; преимущественное качение профилей в окрестности полюса с незначительным скольжением; рациональные условия сопряжения (выпукло-вогнутый контакт во многих фазах зацепления); высокий КПД; пониженная вибрация; улучшенные технологические возможности при изготовлении и упрочнении колес. Расчеты показывают реальную возможность создания циклоидального планетарного редуктора с передаточным отношением в одной ступени i=6–16 и числами зубьев колес кратными 2 и 3 (рис. 4) [8], что значительно превышает возможности аналогичной схемы с традиционным зацеплением (эвольвентным или Новикова) и дает новый импульс к разработке высокоэффективных редукторных турбобуров и скважинных насосов для добычи нефти.
Совершенствование традиционных зубчатых передач и разработка новых типов зацеплений привлекает все большее внимание как в России, так и за рубежом, что связано с влиянием зубчатых механизмов на основные технические характеристики машин, общим научно-техническим прогрессом, развитием материаловедения, станкостроения и цифровых технологий.
Среди появившихся в последнее время в технической литературе и патентном фонде нетрадиционных типов зубчатых передач можно отметить инновационные конструкции колес с радиусным профилем зубьев, состоящим из касающихся дуг окружностей головок и ножек с их центрами на делительной окружности [9] и колес с линией зацепления, выполненной в виде лемнискаты[10]. Авторы этих изобретений обосновывают технические и технологические преимущества своей геометрии по сравнению с эвольвентным профилем и указывают области возможного применения зацеплений.
В настоящей статье предлагается новый альтернативный тип зубчатого зацепления [11], отличающийся тем, что исходный контур зубчатой рейки выполнен в виде гармонической кривой (синусоиды или косинусоиды), смещенной в общем случае относительно производящей прямой, а торцовый профиль зубьев колеса образуется как огибающая семейства гармонических кривых при их обкатке по основной окружности определенного радиуса, выбираемого в зависимости от требуемого числа зубьев колеса. При этом число зубьев колеса может принимать любое значение, начиная от единицы, что создает предпосылки расширения кинематических возможностей зубчатого механизма и получения высокого передаточного отношения в одной ступени.
Главное отличие и преимущество гармонической кривой перед циклоидой состоит в ее плавности, что не требует выполнения процедур эквидистантирования и дает возможность использовать в качестве исходного контура рейки, обкатываемого по основной окружности радиусаrz, непосредственно саму гармонику. Таким образом, при образовании торцового профиля от гармонической зубчатой рейки, подобно случаю эвольвентного зацепления, осуществляется переход от трехступенчатой схемы (рейка — эквидистанта рейки — смещенная эквидистанта) к двухступенчатой схеме (рейка — смещенная рейка), в которой начальный контур рейки I совпадает с исходным контуром II (рис. 5).
Координаты исходного контура гармонической зубчатой рейки относительно производящей прямой (инструментальных осей хрур) можно представить в виде:
где xo, yо — начальные координаты гармоники I, симметрично расположенной относительно производящей прямой; Δx — смещение исходного контура рейки относительно производящей прямой.
Если в качестве гармоники использовать косинусоиду (рис. 5), то
где Ψ — угловой параметр, изменяющийся от 0 до 2π;
r — радиус единичной окружности;
А — амплитуда гармоники, равная половине высоты зубьев рейки;
u — коэффициент типа профиля: u = 1 при образовании эпигармонического профиля (от положительной косинусоиды, когда зуб рейки направлен от центра основной окружности), u = –1 при образовании гипогармонического профиля (от отрицательной косинусоиды, когда зуб рейки направлен к центру основной окружности, рис. 5).
На рис. 6 показаны текущие положения реек при образовании эпи- и гипогармонических профилей при использовании, соответственно, положительной и отрицательной косинусоиды. Отличие между семействами этих кривых, с точки зрения исходного положения рейки, заключается в расположении точки, соответствующей максимальному диаметру профиля: в случае образования гипогармонического профиля данная точка (а, рис.5) расположена на оси хр в начале углового шага рейки (Ψ = 0), в то время как при образовании эпигармонического профиля аналогичная точка будет располагаться в середине углового шага (Ψ = π).
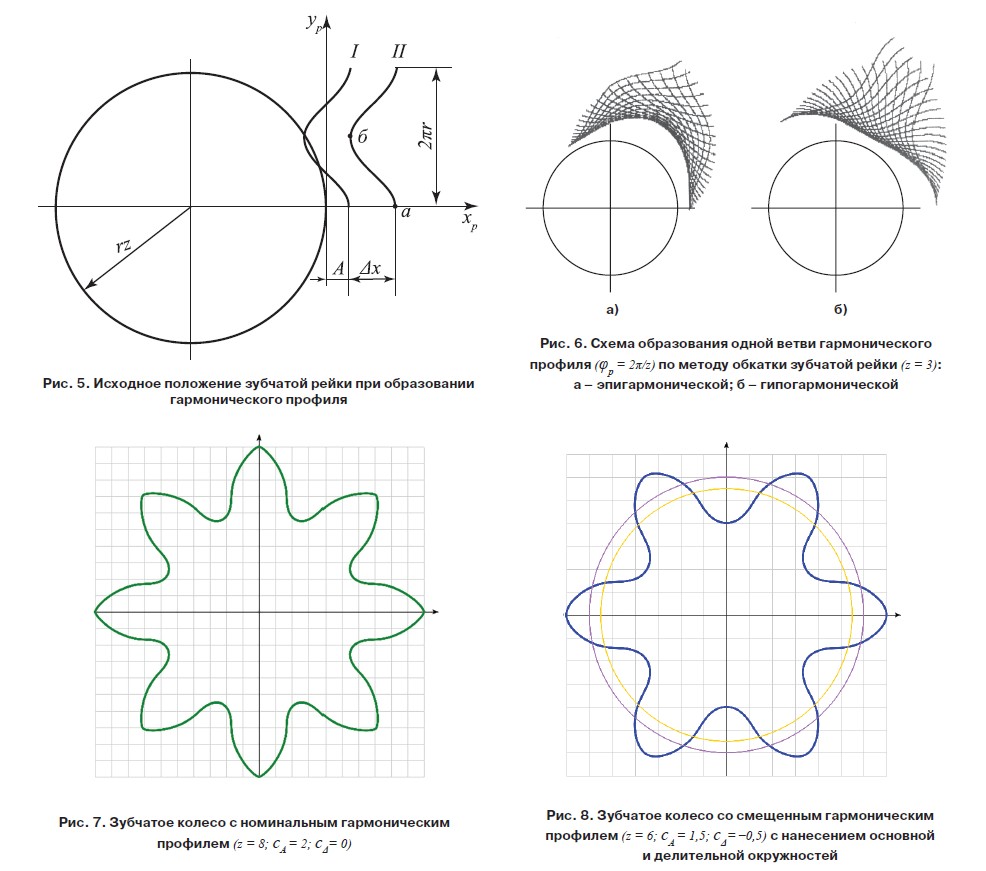
В текущем положении при обкатке по основной окружности производящая прямая и связанная с ней рейка поворачиваются на угол φр. Поскольку обкатка производится без скольжения, семейство кривых рейки описывается следующими параметрическими уравнениями:
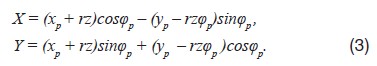
Гармонический зубчатый профиль представляет собой внутреннюю огибающую семейства обкатываемых реек (рис. 6). Для перехода от (3) к уравнению огибающей необходимо установить зависимость между Ψ и φр. Ее можно получить через общие геометрические построения, учитывая, что нормаль к огибающей проходит через полюс — точку касания производящей прямой и основной окружности.
Отличительным свойством замкнутого гармонического профиля является независимость его формы от схемы образования: эпи- и гипогармонические профили получаются идентичными (смещенными по фазе на уголπ/z). Поэтому, в отличие от циклоидального, такой профиль можно назвать общим термином «гармонический», не уточняя, от какой кривой (синусоиды или косинусоиды) образована рейка, и не добавляя приставку эпи- или гипо-.
Средний диаметр гармонического профиля (по делительной окружности зубьев) не зависит от амплитуды гармоники, а высота зубьев — от смещения рейки:
Форма гармонических торцовых профилей пары находящихся в зацеплении зубчатых колес (исходного — индекс 1 и сопряженного — индекс 2) полностью определяется сочетанием трех безразмерных геометрических параметров:
— передаточного отношения i = z2 : z1 ;
— коэффициента формы гармоники сА = А / r ;
— коэффициента смещения исходного контура рейки сΔ = Δx / r.
Выбор численных значений указанных безразмерных геометрических параметров зависит от типа и требуемых характеристик зубчатой пары.
Зубчатые колеса с гармоническим профилем зубьев (рис. 7, 8) могут использоваться в различных механизмах внешнего и внутреннего зацепления с параллельными осями.
В общем случае при выбранном z1-зубом исходном гармоническом профиле колеса (схема построения которого приведена на рис. 5 и 6) сопряженный ему профиль второго колеса образуется как огибающая исходного профиля при обкатке начальных окружностей колес, отношение радиусов которых (a, b) соответствует передаточному отношению: b/a = z2/z1.
На практике при построении сопряженного профиля можно использовать упрощенный метод, при котором сопряженный профиль выполняется аналогично исходному по методу обкатки от общего контура зубчатой рейки[4]. Применительно к предлагаемому зацеплению это означает, что при образовании профилей сопряженных колес форма гармоники остается неизменной (А1 = А2 = А), а меняется лишь величина смещения рейки (Δх1; Δх2) [11].
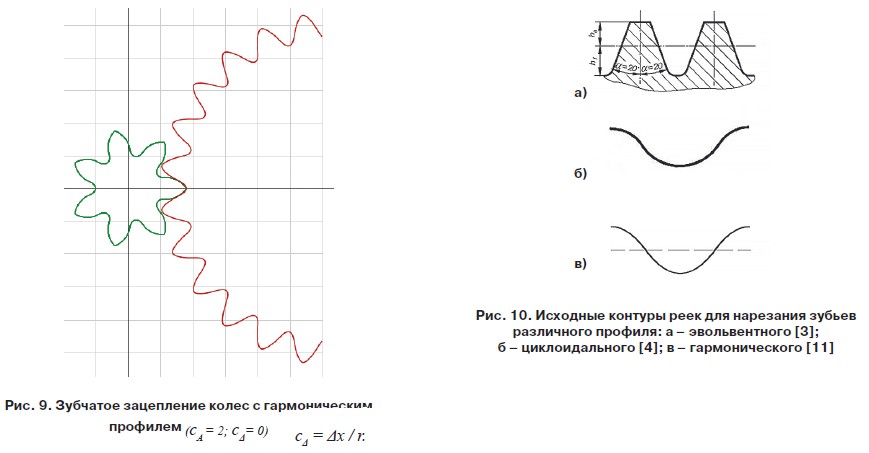
В качестве примера на рис. 9 изображен вариант исполнения зубчатой пары внешнего гармонического зацепления без смещения с передаточным отношением 7:25 в характерной фазе зацепления, соответствующей контакту выступа зуба ведущей шестерни со впадиной зуба ведомого колеса.
При проектировании зубчатых колес с гармоническим профилем форма их зубьев может варьироваться в широких пределах в зависимости от сочетания между размерными параметрами (r; A; Δx) или безразмерными коэффициентами (сА; сΔ), что позволит обеспечить наилучшие показатели зацепления (с геометрической, кинематической и силовой точек зрения), в том числе за счет выбора оптимальной кривизны и относительного скольжения профилей для различных передаточных отношений механизма.
Таким образом, с изменением соотношения между безразмерными коэффициентами профиля, имеется возможность придания зубу различной формы (от плавной до заостренной на вершине) в зависимости от назначения и схемы зацепления (механическая передача или рабочие органы гидромашины), заданной характеристики и условий эксплуатации механизма.
Зацепление с гармоническим профилем зубьев, образованное по методу обкатки зубчатой рейки, аккумулирует в себе положительные свойства аналогичных эвольвентных и циклоидальных зацеплений (рис. 10) и имеет следующие преимущества:
• По сравнению с циклоидальным зацеплением — возможность, как и в случае эвольвентного зацепления, использовать при проектировании и изготовлении сопряженных зубчатых колес внешнего зацепления идентичный для обоих профилей исходный контур рейки. Это обусловлено тем, что начальная гармоническая кривая I (рис. 5) на интервале от 0 до 2π расположена симметрично относительно продольной оси yр и имеет одинаковую кривизну своих вершин, поэтому зубья рейки характеризуются идентичной формой своих выступов и впадин. В случае же внешнего циклоидального зацепления профили колес представлены сопряженными гипо- и эпициклоидальными кривыми (рис. 4), профилирование которых производится от соответствующих исходных контуров.
• По сравнению с эвольвентным зацеплением — возможность вследствие плавности, отсутствия переходных кривых и меньшей склонности к подрезам и заострениям синусоидальной кривой разрабатывать профили колес с минимальным числом зубьев, вплоть до предельных модификаций одно- и двухзубого исполнения в форме кулачка и гитары. Это открывает новые кинематические, конструктивные и технологические возможности при создании зубчатых передаточных механизмов и рабочих органов гидравлических машин с внешним и внутренним зацеплением, в том числе снижение их массогабаритных показателей.
Гармонический торцовый профиль зубьев помимо механизмов с цилиндрическими колесами может также использоваться при разработке конических и червячных передач.
Техническим результатом предложенного типа зацепления является повышение эффективности и гибкости процесса проектирования и изготовления зубчатых колес (в том числе на современном зубообрабатывающем оборудовании), что в перспективе создает реальные предпосылки дальнейшего расширения области применения и совершенствования механических передач и объемных роторных машин в различных отраслях техники.
