Трещиноватость в горном массиве представляет собой совокупность систем трещин, которые в случае нефтяного месторождения играют очень важную роль в миграции и фильтрации флюида. Под трещиной в дальнейшем понимается поверхность раздела в горной породе, по которой может претерпевать разрыв вектор перемещения [1]. Характеристики трещиноватости, такие как раскрытость трещин, их размер, распределение, ориентация и т.д., связаны с характером напряженного состояния, деформационными и прочностными свойствами породы [2]. Большой интерес представляет параметр «раскрытость» трещины, так как он служит основой для оценки проницаемости. Возможность трещине оставаться открытой/проводящей зависит от действующих на нее напряжений, а также и от сил трения и сцепления по плоскости разрыва. Предельное напряженно-деформированное состояние трещины можно описать с помощью линейного критерия прочности, а именно «правилом» Байерли [3] или же нелинейного критерия по модели Бартона [4]. Под термином критически-напряженная или активная трещина далее понимается трещина, находящаяся в состоянии неустойчивого равновесия, в том смысле, что при малом увеличении сдвигового напряжения, превышающем величину произведения нормального напряжения на коэффициент трения, вдоль плоскости трещины возникнет перемещение. На диаграмме Мора критически напряженная трещина находится выше линии сухого трения [5, 6]. Связь критически-напряженных трещин с трещинами, проводящими флюид, была изучена рядом исследователей. Сделан вывод о том, что связь такая существует и имеет высокую подтверждаемость [6, 7, 8]. Одно из объяснений такой связи трактуется следующим образом: увеличение сдвиговой деформации (перемещения по плоскости трещины) приводит к эффекту дилатансии, вследствие которого увеличивается раскрытость трещины. Использование гипотезы о связи критически-напряженных трещин и трещин флюидопроводящих может помочь в решении двух задач: первая – это определение трещин, которые могут проводить флюид на основе данных о напряженно-деформированном состоянии, вторая – это оценка напряженно-деформированного состояния на основе данных о проницаемости трещин. Данный процесс также можно называть калибровкой проводящих на критически-напряженные трещины и наоборот. Ее можно провести на основе данных: керновых исследований [9], промыслово-геофизических исследований [10], интерпретации пластовых микросканеров и специальных методов геофизического исследования скважин (ГИС) [11]. Перечисленные методы являются косвенными и довольно часто интерпретация по нескольким методам в том же интервале может отличаться. Это следует учесть при оценке напряженного состояния трещин.
МЕТОДИКА ИССЛЕДОВАНИЯ
В горном массиве существует ряд структурных неоднородностей различного ранга: тектонические разрывы, трещины. Эти неоднородности выступают в роли плоскостей ослабления: они характеризуются меньшим сопротивлением сдвигу по сравнению с неразрушенной горной породой и оказывают значительное влияние на механические процессы, происходящие во время разработки пласта.
Для изучения влияния параметров трещин на изменение напряженно-деформированного состояния с последующей оценкой характеристик трещин, таких как раскрытость, была построена 3D-геомеханическая модель. В ней свойства материала «сплошной» породы соответствуют свойствам породы, в которой отсутствуют структурные дефекты, и заданы постоянными для всего объема. К таким свойствам относятся: модуль Юнга, коэффициент Пуассона, плотность, константа Био, пористость, предел прочности на сжатие, угол внутреннего трения, предел прочности на растяжение. Свойства материала «трещин» отличаются от «сплошной» породы, они представлены: начальной нормальной и сдвиговой жесткостью, углом трения и когезией. Первые два заданы различными – в зависимости от коэффициента шероховатости трещины.
Предельное напряженное состояние трещин оценивалось на основе нелинейного критерия прочности по модели Бартона. Для использования данного критерия необходимо знать следующие параметры: коэффициент шероховатости стенок трещины, прочность на сжатие материала стенки трещины, эффективное нормальное напряжение, действующее на плоскость трещины и остаточный угол трения [12, 13].
σn – эффективное нормальное напряжение, МПа;
τ – предельно-сдвиговое напряжение, МПа;
JRC – коэффициент шероховатости трещины, д.е.;
JCS – прочность на сжатие материала стенки трещины, МПа;
φост – остаточный угол трения, градусы.
Данный критерий был получен по результатам ряда испытаний на сдвиг пород различного генезиса. Это позволило выявить эмпирическую связь между параметрами трещины и напряженным состоянием образца. Из всех вышеуказанных параметров наибольшей неопределенностью обладает коэффициент шероховатости. Прочность на сжатие материала стенки трещины в большинстве случаев принимается равной UCS (пределу прочности на сжатие), если поверхность трещины не подверглась выветриванию и остаточный угол трения оценивается по методике. С шероховатостью ситуация обстоит сложнее. Во-первых, данный параметр динамический и меняется как в процессе, так и после возникновения подвижки по разрыву, а во-вторых, его оценка не прямая и основывается на косвенных исследованиях [14, 15, 16]. В абсолютных величинах этот коэффициент меняется от 0 до 20.
В данной работе было оценено предельное сдвиговое напряжение с учетом изменения коэффициента шероховатости системы трещин в диапазоне от 2 до 18 с шагом 2. Прочность на сжатие материала стенки трещины принята равной 35 МПа, остаточный угол трения 20 градусов. Основные три этапа моделирования включали: построение дискретной модели сети трещин (DFN), 3D-конечно-элементное геомеханическое моделирование различных кейсов при изменении параметров материала «трещин» и оценка напряжений, действующих на плоскость трещины с расчетом механической и гидравлической раскрытости.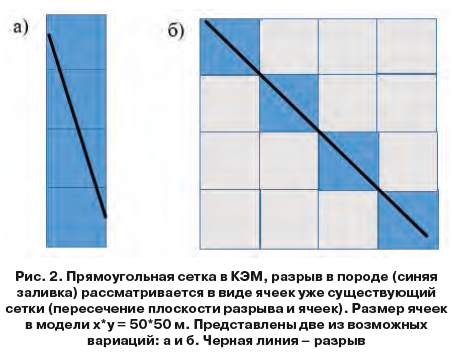
ПОСТРОЕНИЕ МОДЕЛИ ТРЕЩИНОВАТОСТИ
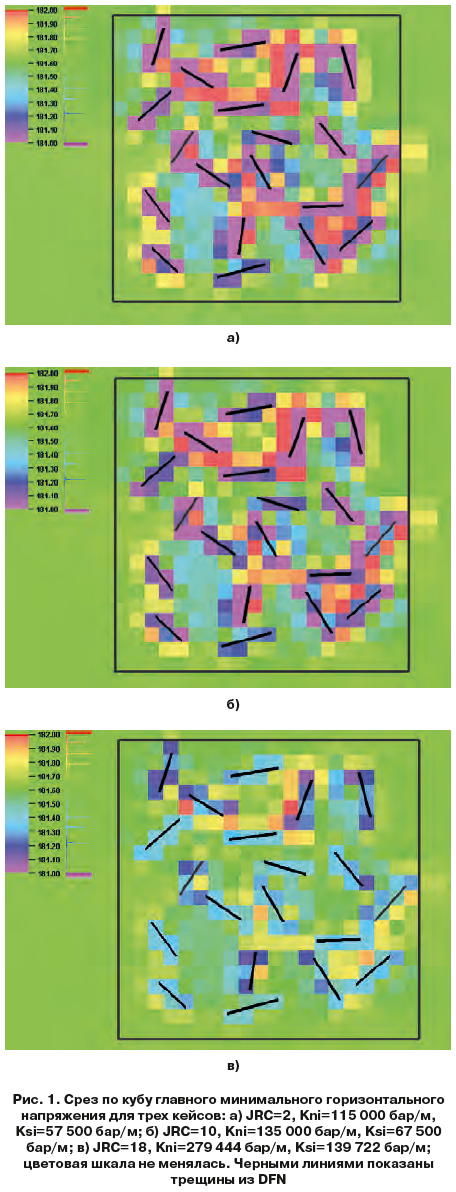
Модель трещиноватости построена с использованием детерминистического подхода (DFN – на базе платформы Petrel), в котором необходимо предварительно подготовить данные трещин в виде поверхностей или полигонов [17]. В этой работе использовались полигоны, геометрические характеристики, такие как пространственное расположение и ориентация были заданы вручную и имеют случайный характер. Угол падения плоскости трещин варьируется в пределах 20 – 90 градусов, азимут падения 0 – 360 градусов, длина трещин – 100 м. Модель трещин создана в зоне детальной геомеханической сетки Z=1000 м – 1050 м. Визуальное представление модели трещин приводится на рис. 1, вид сверху, совместно с результатами моделирования напряженного состояния.
Трещины как элементы, которые характеризуются другими деформационными и прочностными свойствами по отношению к «сплошной» породе (intact rock) оказывают значительное влияние на напряженно-деформированное состояние резервуара. По этой причине они должны быть включены в геомеханическую модель. Существует три подхода к моделированию разрывов в геомеханической сетке. В данной работе в программном пакете Petrel используется прямоугольная сетка и разрыву присваиваются ячейки уже существующей сетки. Несмотря на то, что разрыв представлен в виде ячеек – это отдельный объект, которому соответствует материал типа «трещина». На рис. 2 приводятся два примера модели разрывов, «вид» разрыва будет зависеть от конфигурации ячеек, которые он пересекает. Стоит отметить, что в данном подходе моделирования также учитывается влияние ориентации разрыва (угол и азимут падения) на напряженно-деформированное состояние. Тем самым, несмотря на то, что визуально два разрыва могут иметь одинаковую конфигурацию в модели (тот же объем и геометрия ячеек), в случае различных углов падения/азимутов плоскости разрыва, напряженное состояние будет отличаться. Детальное описание недостатков и достоинств данного подхода моделирования разрывов приведено в работе [18].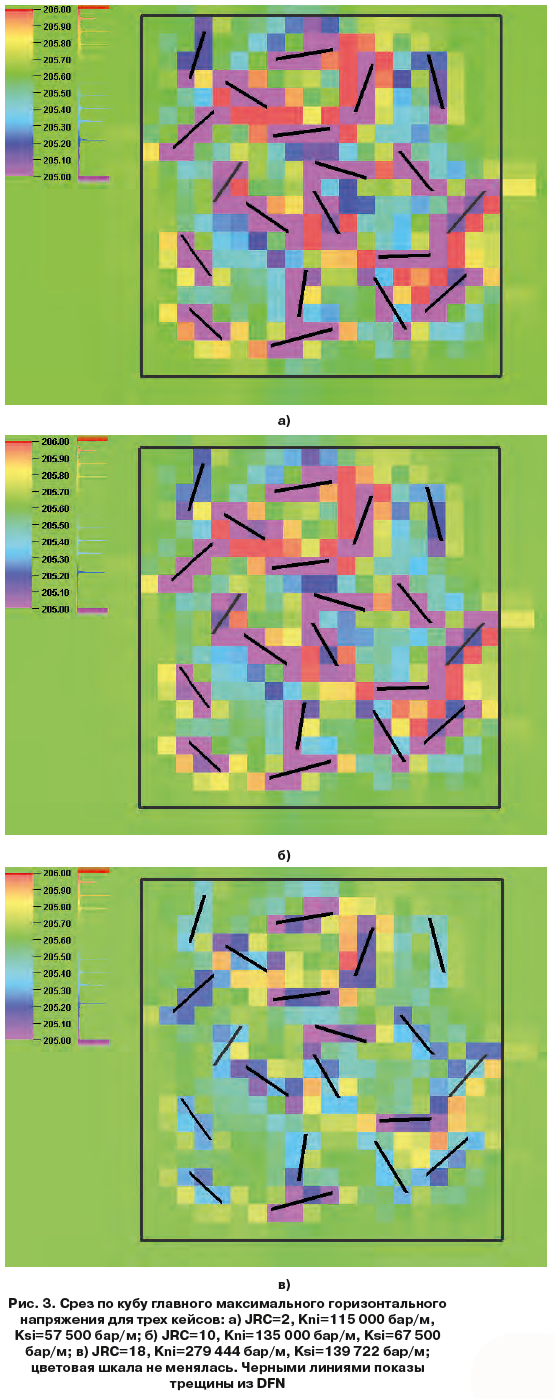
В 3D-конечно-элементной модели стандартно деформационные свойства разрывов необходимо задать перед выполнением расчета в симуляторе [19]. Они представлены следующими характеристиками: начальная нормальная и сдвиговая жесткости, угол внутреннего трения и когезия. Предложение по использованию параметров жесткости для описания напряженного состояния разрыва принадлежит Р.Гудману [20]. В этой работе параметр начальной нормальной жесткости трещины был рассчитан эмпирическим путем [21] по (2), тогда как начальная сдвиговая жесткость была принята 0,8 от начальной нормальной жесткости, а угол трения равным 20 градусам. Далее данное значение угла трения (в виде остаточного угла трения) использовалось для расчета сдвигового напряжения по модели Бартона (1):
Kni – начальная нормальная жесткость.
Как видно из (2) для расчета начальной нормальной жесткости (Kni) необходимо знать коэффициент шероховатости (JRC, д.е.), прочность на сжатие материала стенки трещины (JCS, МПа) и начальное раскрытие (E0, мм).
Для изучения влияния коэффициента шероховатости на НДС в поле 3Д были определены параметры жесткости для кейсов: JRC=2; 4; 6; 8; 10; 12; 14; 16; 18 и подготовлены соответствующие материалы для дальнейшего моделирования. В итоге проведено 9 численных симуляций и по каждой оценивались действующие напряжения на плоскости трещины и параметры: механическая и гидравлическая раскрытость.
КОНЕЧНО-ЭЛЕМЕНТНОЕ МОДЕЛИРОВАНИЕ НДС
Расчет напряженно-деформированного состояния выполнялся на основе метода конечных элементов. Первым этапом являлось построение структурного каркаса и сетки. Для этого были заданы 2 горизонта на абсолютных глубинах Z= –1000 м и –1050 м, размер ячеек сетки x*y*z = 50 м *50 м * 0,5 м, площадь полигона моделирования 0,01 км2. Для корректного расчета напряженно-деформированного состояния построена вмещающая среда, проведено наращивание сетки до Z= 0 и Z= –1500 м по вертикали с геометрическим фактором равным 1,2. Наращивание на гранях модели (по периферии) выполнено на расстоянии равным 1 км с геометрическим фактором 1.4. В результате модель состояла из резервуара (область построения модели трещиноватости – зона по Z = –1000 м – 1050 м) и вмещающей среды.
Механические свойства, необходимые для расчета напряженно-деформированного состояния, а именно: модуль Юнга, коэффициент Пуассона, предел прочности на сжатие и растяжение, угол внутреннего трения были заданы постоянными для всего объема и приведены в табл. 1. Что же касается материала трещин, как было указано ранее, проведен предварительный расчет параметров жесткости по (2) для различных JRC, и для каждого варианта материала выполнен расчет в симуляторе с оценкой НДС. Подробные характеристики материалов трещин приведены в табл. 2, Модель трещин учтена в том виде, который описывался выше и приведена на рис. 1. Поровое давление принято равным гидростатическому и задано в виде градиента 0.1 бар/м. Что же касается задания условий нагружения, то в Visage используются три подхода: нагружение через напряжения (два полных горизонтальных напряжения), деформации и тензор полных напряжений. В данном случае применен второй подход: минимальная горизонтальная деформация принята 0,0001, максимальная – 0,0002, азимут простирания максимального горизонтального напряжения – 130 градусов.
Результатом конечно-элементного моделирования являются кубы: компонент тензора полных и эффективных напряжений, тензора деформаций, перемещений (x,y,z), а также сдвиговых и нормальных перемещений по модели трещин. В 3D-геомеханической модели трещины – это элементы среды, которые вносят «возмущение» в напряженно-деформированное состояние. Для исследования данного «возмущения» свойства материала сплошной/неразрушенной породы были заданы постоянными. Изменение напряженного состояния связано в таком случае только с наличием трещин и со свойствами трещин. На рис. 1, 3 показаны срезы на глубине Z= –1025 м по кубу главного минимального напряжения и максимального напряжения для трех кейсов: JRC=2; 10; 18. Расчет главных напряжений проведен по (3) и (4):
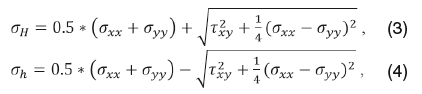
σxx,σyy,τxy – компоненты тензора эффективных напряжений по 3-D модели.
По каждому срезу отмечается локальное изменение напряжения в зоне, где наблюдается трещина.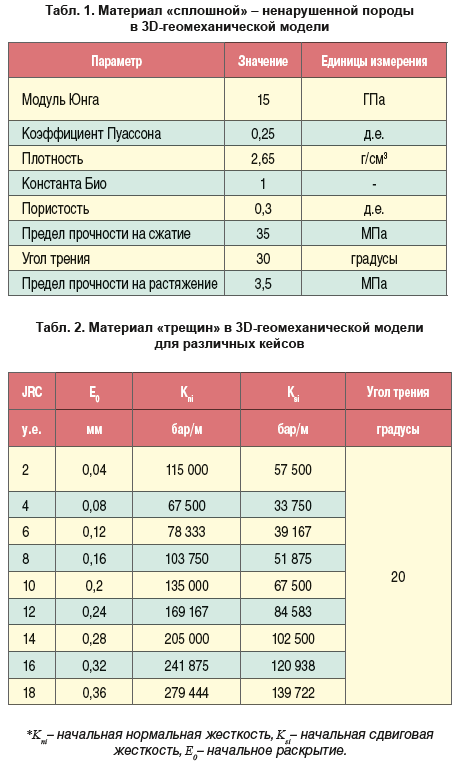 
Можно отметить, что вдоль трещины напряжение уменьшается, достигая минимальных значений, тогда как в ячейках, которые соответствуют «кончику» трещины, напряжение увеличивается, достигая максимальных значений. Распределение напряжений носит различный характер от одной трещины к другой, но в целом первые два наблюдения сохраняются. Что же касается неравномерного поля напряжений и изменчивости от одной трещины к другой, то это можно объяснить тем, что в симуляторе учитывается не только ячейка в виде геометрической характеристики, которой присваивается другой материал, но и ориентация трещины в данной ячейке. Тем самым трещины, которым соответствуют одинаковые ячейки и материал, будут влиять на напряженное состояние, исходя также и из особенностей ориентации плоскости (угол и азимут падения). На рис. 1, 3 с результатами моделирования разных кейсов можно увидеть, что коэффициент шероховатости также влияет на изменение НДС посредством параметров жесткости трещин. С увеличением шероховатости растет жесткость трещины и тем самым трещины с низким JRC и параметрами жесткости оказывают большее влияние на изменение напряженного состояния, чем трещины с высоким JRC.
Следующим этапом работы была задача непосредственно оценить напряжения, которые действуют на плоскость трещины (нормальное и сдвиговое напряжение) по данным 3D-моделирования. Для этого использовались кубы компонент тензора эффективных напряжений. Расчет напряжений на плоскость трещины можно разделить на несколько этапов. Первый заключается в определении системы координат, в которой находится плоскость. Данная система описывается тремя осями, которые отличаются от осей географической системы координат. Трещину можно охарактеризовать вектором нормали к плоскости трещины (nn), вектором простирания (ns), вектором падения (nd). Расчет каждой величины приводится в (5) – (7) «dip» – угол падения, «strike» – азимут простирания.
Вторым этапом является определение компонент вектора напряжения на основе данных 3D-геомеханической модели:
В данном случае индексы 1, 2, 3 соответствуют компонентам вектора нормали.
Третий этап включает расчет сдвигового напряжения, действующего на плоскость трещины. В данном случае у сдвигового напряжения есть две составляющие, одна совпадает с линией падения (τd), вторая с линией простирания (τs).
Полное сдвиговое напряжение определяется как корень суммы квадратов двух компонент напряжений.
Существует еще один способ оценки сдвигового напряжения через нормальное напряжение и компоненты вектора напряжений:
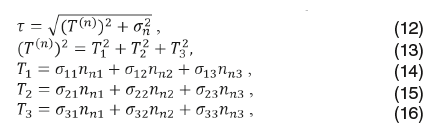
T1,T2,T3- компоненты вектора напряжений.
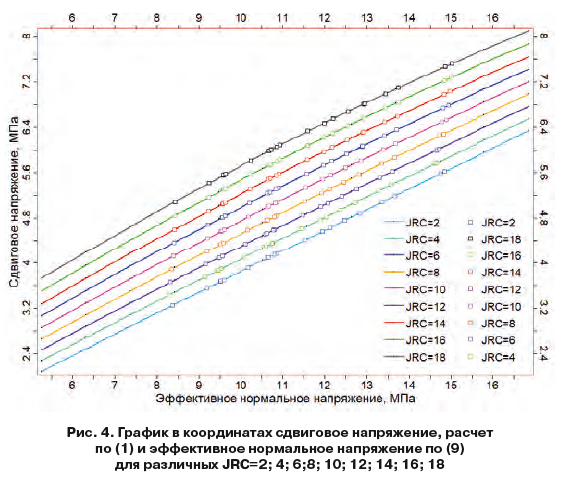После применения вышеописанного подхода были рассчитаны нормальное и сдвиговое напряжения, действующие на плоскость трещины. Каждой трещине по результатам моделирования соответствовало одно значение сдвигового и нормального напряжения. По модели Бартона (1) определен предел прочности трещины на сдвиг для различного значения коэффициента шероховатости: JRC=2; 4; 6; 8; 10; 12; 14; 16; 18 и нормального напряжения (9 кейсов) по результатам 3Д-моделирования. Чувствительность критерия прочности Бартона к входным данным (коэффициент, шероховатость, прочность на сжатие материала стенки трещины, эффективное нормальное напряжение) подробно описана в работе [22]. Результат расчета критерия прочности на сдвиг проиллюстрирован на рис. 4. Можно отметить, что для JCS=35МПа (JCS больше действующих эффективных нормальных напряжений), увеличение коэффициента шероховатости приводит к увеличению сопротивления сдвигу по трещине. Тем самым для активации трещины с JRC=2 требуется приложить меньше усилий, чем для активации трещины с JRC=18. Данный вывод также коррелирует с определением начальной жесткости трещины (2) (табл. 2), исключение составляет кейс с JRC=2. В данном случае жесткость трещины превышает значения параметра жесткости для кейсов JRC=4; 6; 8.
ОЦЕНКА РАСКРЫТОСТИ И ПРОНИЦАЕМОСТИ
Раскрытость трещины – параметр комплексный и динамический, он характеризует среднее расстояние между стенками трещины или же ширину зоны «контакта». По многочисленным исследованиям отечественных и зарубежных авторов, возникновение раскрытости по трещине обусловлено деформациями сдвига и отрыва, которые трещина может испытать [21, 23]. Широкое распространение получила модель Бартона-Бандиса, где авторы ввели понятия механической и гидравлической раскрытости. Данные характеристики являются производными напряженно-деформированного состояния и свойств трещины, таких как шероховатость и прочность. Для расчета механической раскрытости E необходимо предварительно оценить E0 – начальное раскрытие, мм; En – величину сжатия берегов трещины под действием нормальных напряжений σn; Ed – величину раскрытия, обусловленную дилатансией, мм.
Расчет начального раскрытия E0 основан на знании коэффициента шероховатости – JRC, предела прочности на одноосное сжатие – UCS и прочности материала стенки трещины – JCS. По исследованиям авторов [4] JCS принимается равным UCS в большинстве случаев, когда трещиноватая порода не подверглась выветриванию. Такое допущение было принято и в данной работе. Результаты расчетов начального раскрытия приводятся в табл. 2 для различных JRC.
Величина сжатия берегов трещины Еn является производной: σn’ – эффективного нормального напряжения, МПа, Kni – начальной жесткости, МПа/мм и Cm – максимального возможного сжатия берегов трещины, мм: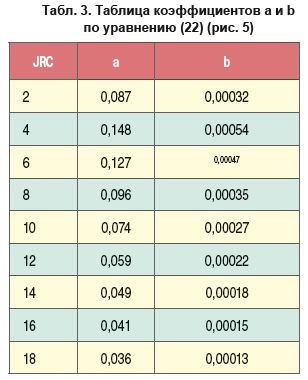
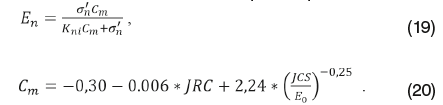
Процесс расчета начальной жесткости трещины был описан ранее (2). Следует отметить, что (19) и (20) установлены в случае: JRC= 5- 15, JCS= 22 – 182 МПа и Е0 =0.10 – 0.60 мм. При использовании этих же уравнений для JRC= 2 – 4 величина сжатия берегов трещины превышает начальное раскрытие, и механическое раскрытие является отрицательным.
Величина раскрытия, обусловленная сдвиговой деформацией (Ed), является функцией Usp – сдвигового перемещения, мм и динамического угла дилатансии – φdm. Последний, в свою очередь, оценивается по динамическому коэффициенту шероховатости JRCm [4].
Определение динамического коэффициента шероховатости проводится в лабораторных условиях, путем построения графика в координатах сдвиговое напряжение и перемещение вдоль трещины (мм) или путем сканирования поверхности трещины до и после испытания на сдвиг. В данной работе сделано допущение о том, что JRCm уменьшился на 0,25 относительно начального JRC для каждого кейса, к примеру, для JRC=2, JRCm будет 1,75.
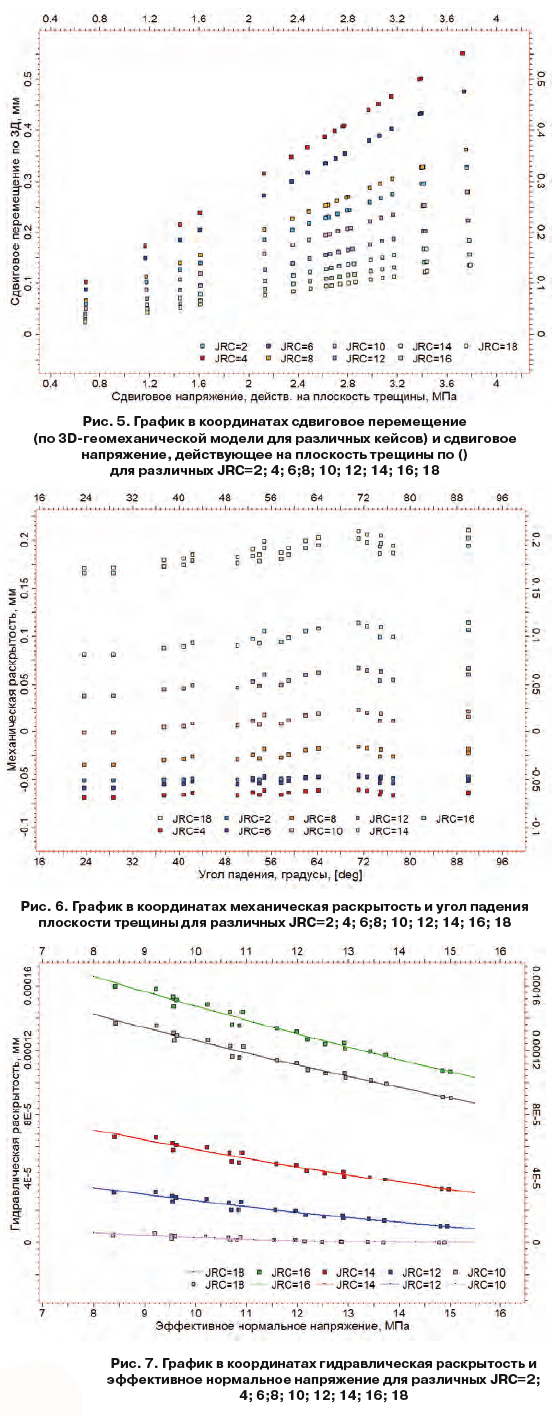
Сдвиговое перемещение по плоскости трещины было получено в ходе 3Д-конечно-элементного моделирования. Как указывалось, ранее проведен расчет 9 кейсов для различных JRC, что позволило оценить величину раскрытия для каждой симуляции. На рис. 5 приводится график в координатах: сдвиговое перемещение по 3Д модели (мм) и сдвиговое напряжение, действующее на плоскость трещины, рассчитанное по (12). Увеличение сдвигового напряжения приводит к росту сдвиговых перемещений, эта связь характеризуется как линейная и имеет следующий вид:
Коэффициенты a и b для различных JRC представлены в табл. 3. По рис. 5 можно сделать вывод о том, что с увеличением коэффициента шероховатости уменьшается сдвиговое перемещение. Это можно объяснить увеличением жесткости трещины по мере роста шероховатости. Также отмечается равномерное увеличение сдвигового перемещения по той же трещине для JRC=18; 16; 14; 12; 10; 8; 2 и резкое увеличение (скачок) перемещения для JRC=4 и 6 относительно остальных графиков. Сдвиговое перемещение меняется от 0 до 0,4 мм в случае JRC=18; 16; 14; 12; 10; 8; 2 и достигает максимальных значений для JRC=4 и 6 в диапазоне 0 – 0,55 мм.
После расчета начального раскрытия (18), величины сжатия берегов трещины (19) и величины раскрытия, обусловленной сдвиговой деформацией (21), определено механическое раскрытие для каждой трещины в отдельности. На рис. 6 показан график в координатах – механическая раскрытость (мм) и угол падения трещины (градусы). С увеличением угла наклона трещины наблюдается рост раскрытости, но данную связь проблематично охарактеризовать определенной функцией (линейной или степенной). Так как встречаются участки, где тенденция роста изменяется, это наблюдение позволяет сделать вывод о том, что недостаточно знать угол падения трещины для восстановления параметра раскрытия. Напряженное состояние, посредством которого выражается раскрытость, является комплексной величиной чувствительной не только к углу падения, а также и к азимуту трещины (рис. 1, 3) относительно направления максимального горизонтального напряжения. Шероховатость значительно влияет на раскрытость: с ростом шероховатости трещины увеличивается механическая раскрытость. Но в случае JRC= 2; 4; 6; 8, при тех граничных условиях, которые были заданы в 3Д-геомеханической модели (минимальная горизонтальная деформация = 0,0001, максимальная = 0,0002, азимут простирания максимального горизонтального напряжения = 130 градусов) и свойств материалов (табл. 1, 2), получены отрицательные значения механического раскрытия. Это позволяет сделать вывод о том, что напряженное состояние трещины и способность активации находится в тесной взаимосвязи с параметром JRC. Далее приведен расчет гидравлической раскрытости уже для JRC=10; 12; 14; 16; 18.
Гидравлическая раскрытость (раскрытие, по которому происходит фильтрация флюида) отличается от механической. Это объясняется неровностями/шероховатостью поверхности стенки трещины. Данное концептуальное представление гидравлической раскрытости предлагается по модели Бартона-Бандиса. Авторами была предложена формула расчета гидравлической раскрытости e через механическую E.
(23)
На рис. 7 представлены результаты расчета в диапазоне эффективных нормальных напряжений 8,2 – 15МПа, отмечается, что с увеличением эффективного напряжения гидравлическая раскрытость уменьшается. Минимальные значения раскрытости наблюдаются в случае JRC=10 и максимальные для JRC=18, достигая величины 0,00016 мм. Связь между раскрытием и эффективным нормальным напряжением нелинейная. Максимальное изменение гидравлической раскрытости наблюдается для JRC=16 и 18. Отсюда можно сделать вывод о том, что при уменьшении коэффициента шероховатости параметр раскрытости изменяется в меньшей мере при росте эффективного нормального напряжения. В случае JRC=10 изменение раскрытости незначительное и составляет менее 1e-5.
ВЫВОДЫ
На основе 3D-конечно-элементной модели выполнена оценка напряженно-деформированного состояния системы трещин и проанализировано влияние свойств трещин, таких как начальная жесткость, на минимальное и максимальное горизонтальное напряжение для различных JRC. Выявлено, что с увеличением JRC наблюдается меньшее влияние на НДС в области трещин, что связано с увеличением начальной жесткости трещины, которая рассчитывалась эмпирическим путем. По результатам моделирования для всех трещин было характерно уменьшение напряжения вдоль трещины и увеличение в ячейках на кончике трещины. Предельное напряженное состояние трещины оценивалось с помощью нелинейного критерия прочности Бартона. Отмечается увеличение сопротивления сдвигу по трещине при увеличении JRC, тем самым трещины с более низким JRC легче активировать при равных параметрах: JCS (в данном случае выше, чем действующие нормальные напряжения), остаточный угол трения.
Для расчета раскрытия трещины использовалась модель Бартона-Бандиса. Для этого были необходимы данные компонент тензора эффективных напряжений и сдвиговых перемещений для трещин по 3D-геомеханической модели. Проведено 9 численных симуляций для кейсов JRC=2; 4; 6; 8; 10; 12; 14; 16; 18, отличающихся по параметрам жесткости трещин. Для каждого кейса определены нормальные и сдвиговые напряжения, действующие на плоскость трещины, а также сдвиговые перемещения, которые участвовали в расчете раскрытости. Сдвиговые перемещения по 3D увеличиваются при уменьшении JRC и связаны линейной функцией со сдвиговыми напряжениями, увеличение которых приводит к росту сдвиговых перемещений. Выявленные зависимости можно далее использовать для восстановления значений сдвиговых перемещений в условиях схожих механических свойств с модельными данными. В работе приводится оценка механической и гидравлической раскрытости. Механическое раскрытие для кейсов JRC=2; 4; 6; 8 является отрицательным. Это связано с тем, что начальное раскрытие меньше нормального сжатия берегов трещины, которое зависит от эффективного нормального напряжения. Максимальное механическое раскрытие характерно для JRC=18 и 16 более 0,15 мм. Не удалось установить прямую связь между данным параметром и углом падения трещины, но в целом увеличение угла связано с большим раскрытием. Гидравлическая раскрытость оценивалась для JRC=10; 12; 14; 16; 18, максимальные значения достигнуты для JRC=18 и 16 и она уменьшается с увеличением эффективного напряжения, наиболее существенные изменения наблюдаются при росте JRC.
Описанный подход и полученные результаты позволяют сделать вывод о том, что необходимо учитывать коэффициент шероховатости трещины для оценки напряженно-деформированного состояния трещиноватого массива. 3D-геомеханическое моделирование позволяет оценить механическую и гидравлическую раскрытость на основе данных о напряженном состоянии и сдвиговых перемещениях.
