К вопросу о расчете и методе испытаний насосов на ГЖС
On the issue of calculation and test method for pumps at work in gas-liquid mixture
V. GILEV, A. RABINOVICH, A. IVASHOV «Novomet-Perm» CJSC
S. AGEEV, «OKB BN Konnas» OJSC
Результаты экспериментов по определению распределения давления в насосе из 160 ступеней ВНН5-50 обработаны с использованием предложенной ранее методики расчета насоса при работе на ГЖС, основанной на некой характеристике ступени Hст-f(β,P).

По расчетным данным построены графики распределения по длине насоса величин: газосодержания, напора единичных ступеней, плотности ГЖС. На основании обработки данных серии экспериментов построены зависимости напора ступеней от давления при заданных β.

Ч.2. Применение метода расчета к обработке данных по распределению давления в длинных сборках, см. Ч.1, №2, 2012.
As per calculation data along pump’s length there are drawn distribution graphs of the following values: gas content, thrust of single stages, density of gas-liquid mixture. Results of experiment series are represented as dependences of head of stages on pressure at prefixed β.
Одним из факторов, осложняющих работу УЭЦН, является влияние свободного газа, которое определяется не только величиной входного газосодержания βвх, но и целым рядом других параметров: давлением на входе в насос, дисперсностью и пенистостью смеси, числом и конструкцией ступеней, условиями подвода смеси к входу насоса [1 – 11]. Результаты испытаний на ГЖС также зависят от потребного напора гидравлической системы стенда [12 – 15]. Существенное влияние оказывает плотность газа [16].

В первой части статьи [15] предложен метод расчета работы насоса на ГЖС по некой характеристике единичной ступени. Предложена также методика испытаний для получения этой характеристики. Для реализации предложенной методики необходимо раздельно управлять как минимум тремя параметрами: газосодержанием на входе βвх, давлением на входе в насос Pвх и на выходе из насоса Pвых, что является достаточно сложной технической задачей.

В настоящей работе предпринята попытка получить информацию о виде характеристики единичной ступени из результатов традиционных испытаний длинных сборок, в которых фиксируется распределение давления по длине.

В работе использован метод расчета, предложенный в [15].

В [15] по зависимости Hст-f(β,P) строится среди прочих функция распределения давления1 по длине насоса P-f(N). Функция Hст-f(β,P) имеет смысл некой характеристики единичной ступени и имеет вид поверхности в трехмерном пространстве Hст-P-β. В настоящей статье мы по функции P-f(N) строим функцию Hст-fкр(β,P). Где Hст-fкр(β,P) имеет смысл зависимости напора2 от газосодержания и давления для ступеней насоса, испытанного при конкретных условиях на входе в насос, и представляет собой пространственную кривую (далее – 3D кривую), проходящую по поверхности Hст-f(β,P).

Предполагаем, что по серии кривых Hст-fкр(β,P) можно построить Hст-f(β,P). Показать такую возможность – задача этой статьи.

Методически это выполняется в следующей последовательности. Сначала проводится тщательная экстраполяция экспериментальных кривых P = f(N). В результате функция P = f(N) задается численно с помощью экстраполирующих функций, и мы получаем численные значения P для каждого N. Далее можно вычислить разницу между давлениями соседних ступеней, то есть фактически функцию распределения Hст = Pn – Pn-1 по длине насоса. Остальные параметры рассчитываются по стандартной методике расчета [15] (1 – 4).

Идея расчета и сами расчеты просты. Принцип пошаговый. Каждая ступень повышает давление, при этом уменьшается объем газа, в соответствии с изменением β и P меняется напор, создаваемый соответствующей ступенью.

Предполагаем [15], что напор насоса – простая сумма напоров, создаваемых отдельными ступенями, а срыв происходит только из-за невыполнения условия

∑1N Hn ≥ HC.

где HC – потребный напор гидравлической системы.

В основе расчетов лежит закон Бойля – Мариотта: pV = const.

Напор Hст, создаваемый ступенью под номером N Hст, вычисляется по известным Pn и Pn-1

Hст = Pn – Pn-1. (1)

В остальном процедура расчета соответствует описанию, данному в [15].

На входе в ступень n-1 газосодержание βn-1. Соответственно, в единице объема ГЖС на входе VГ1 = βn-1 и VВ = 1-βn-1. Затем считаются эти же величины на выходе из этой ступени и, соответственно, на входе в последующую ступень n.

Объем газа на выходе ступени n-1 в соответствии с законом pV = const будет равен

VГ2 = Pn-1*βn-1/Pn. (2)

Объем воды не изменяется, поэтому сумма объемов воды и газа на выходе составит

VГ2+ 1-βn-1. (3)

Газосодержание на выходе ступени n-1 и входе в ступень n:

βn= (Pn-1*βn-1/Pn )/(Pn-1*βn-1/Pn + 1-βn-1). (4)

Далее цикл счета повторяется, в нем используются новые значения Pn+1 и Pn, взятые из численной экстраполяции экспериментальной кривой P-f(N) и полученное в предыдущем цикле расчета значение газосодержания βn.

В данном варианте расчета, зная функцию P = f(N), полученную замерами давления вдоль длины насоса при заданных βвх и Pвх и числе ступеней N, мы можем получить информацию о распределении вдоль длины насоса таких параметров, как газосодержание, напор единичных ступеней, плотность ГЖС, а также взаимозависимости этих параметров между собой и давлением. 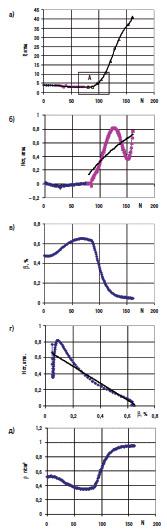 Рис. 1. График P = f(N) (а) и полученные из него расчетом графики Hст = f(N) (б), β = f(N) (в), Hст = f(β) (г), β = f(N) (д) для сборки N = 160 ступеней ВННП5А–50 при Qж.нач. = 50 м3/сут., βвх = 50%, Pвх = 4 атм. Исходные данные – из испытаний на смеси «вода–воздух–ПАВ» На рис.1 приведены в качестве примера результаты подобного расчета для сборки из 160 ступеней ВННП5А-50, испытанной на ГЖС при Qж.нач = 50 м3/сут., βвх = 50%.

Исходный график P = f(N), полученный в эксперименте, приведен на рис. 1а, график изменения значений Hст = Pn-Pn-1 по длине насоса – на рис. 1б. В соответствии с падением давления на участке диспергирующих ступеней происходит рост газосодержания (рис. 1в), затем, начиная примерно со ступеней с номерами около 70, газосодержание уменьшается. Соответственно ведет себя и график изменения плотности ГЖС, рис. 1д.

При обработке кривой 1а получены высокие значения Hст на рис. 1б и рис. 1г на уровне 0,8 атм. Однако осредненные величины, полученные обработкой данных прямолинейными трендами, не выходят за рамки привычных показателей.

Наиболее значимый результат подобной обработки функции P = f(N) представлен на рис. 1г, который прежде всего подтверждает возможность работы обычных ступеней ВНН при высоких газосодержаниях на входе в ступень. Ступени могут создавать напор даже при β~65%. Постепенное увеличение создаваемого единичной ступенью напора с уменьшением β, можно объяснить влиянием соответствующего изменения плотности ГЖС.

Отклонения от монотонной зависимости напора ступеней от газосодержания, рис. 1г, в данной статье мы не обсуждаем. Отметим только, что максимум на кривой Hст = f(β) на рис. 1г в районе 3 – 5%, возможно, является аналогом пиков на кривых, обнаруженных ранее при испытаниях пятиступенчатых сборок малорасходных центробежно-вихревых ступеней на ГЖС «вода–воздух» в том же диапазоне газосодержаний [12].

Следует отметить, что график Hст = f(β) (рис. 1г) в данном случае является проекцией 3D кривой Hст = fкр(β, P) на плоскость Hст-β трехмерного пространства Hст-β-P. Проекция этой же 3D кривой Hст = fкр(β, P) на плоскость β-P имеет следующий вид (рис. 2).

Если 3D кривые Hст = fкр(β, P) расположены на 3D поверхности Hст = f(β, P), то по серии 3D кривых в принципе можно построить искомую 3D поверхность.

Описанная методика имеет ряд недостатков, но она принципиально возможна, что доказывается обработкой результатов серии экспериментов на длинной сборке. К преимуществам методики можно отнести то, что при повышенных Pвх испытания длинных сборок осуществить проще, чем коротких. Это следствие того, что на длинных сборках низки значения газосодержания на выходе βвых (рис. 1в и 3). Тем самым обеспечивается большее гидравлическое сопротивление крана задвижки и, соответственно, более высокие значения hдин и выполняется требование: «…обеспечение необходимой величины потребного напора гидравлической системы стенда (отсутствие недогрузки насоса во время испытаний)» [15]. 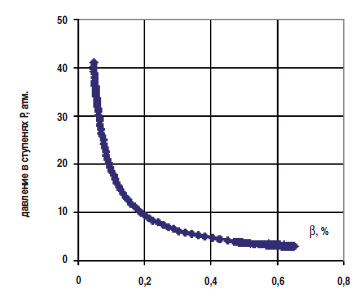 Рис. 2. Проекция на плоскость β–P 3D кривой Hст = fкр(β, P), построенной по экспериментальным данным испытания насоса 160 ступеней ВННП5А–50 при Qж.нач. = 50 м3/сут., βвх = 50%, Pвх = 3 атм Напомним, что потребный напор гидравлической системы HC

HС= hст + hдин = hст+kQ2. (5)

В [15] было показано, что при увеличении Рвх, и при отсутствии (или малой высоте) столба ГЖС на выходе из насоса величина hст отрицательна и есть риск получения отрицательных значений HC. Такой риск уменьшается с ростом hдин при снижении газосодержания на выходе из насоса, т. к. в этом случае величины hдин достаточно, чтобы получить положительные HC. при сложении hдин с отрицательным hст.

На рис. 3 приведены данные расчета для газосодержания на выходе из насоса в виде зависимостей βвых от βвх при различных Qж.нач для всех серий экспериментов. Кривые при Qж.нач = 16, 25 и 35 м3/сут. почти сливаются, а при Qж.нач = 50, 60 и 75 м3/сут. идут тем выше, чем больше величина Qж.нач, что является следствием меньшей напорности ступеней в этом случае. Перегибы на кривых (рис. 3) при Qж.нач = 50, 60 и 75 м3/сут. объясняются появлением при больших βвх участков диспергирования, как на рис. 1а, то есть неучастием значительной части длины насоса в процессе сжатия ГЖС. 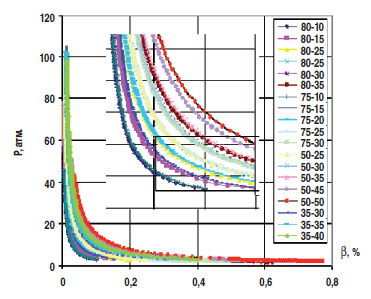 Рис. 3. Газосодержание на выходе из сборки 160 ступеней ВНН5–50 βвых в зависимости от газосодержания на входе βвх для серий опытов с различными положениями задвижки. Цифры в рамке – значения Qж.нач. Несмотря на описанное преимущество длинных сборок, выражающееся в малых значениях βвых, на данный момент нам кажется более привлекательной методика замеров серии кривых Hст = f(β) при разных давлениях Pвх, с замерами давлений на входе и выходе при использовании коротких сборок [15].

Дело в том, что при испытаниях длинной сборки мы получаем серию 3D кривых Hст = fкр(β,P), имеющих сложную траекторию в пространстве H-P-β. В случае серий испытаний коротких сборок при заданных Pвх эти траектории практически расположены в плоскостях, параллельных плоскости β-P.

В вопросе о работе насоса на ГЖС особый интерес представляет влияние давления на входе в насос. В настоящей работе была проведена попытка выявить влияние текущих значений давления в ступенях на текущие значения напора, создаваемого отдельными ступенями, по данным обработки кривых P-f(N), полученных в экспериментах с длинной сборкой.

Использовали экспериментальные данные, полученные обработкой массива кривых, подобных кривой рис. 1а. Эксперименты проведены на стенде [10] при избыточном давлении на входе 3 атм.

Как можно видеть на рис. 4 (координаты β-P), все экспериментальные данные укладываются в довольно узкую область. Мы ограничились малой областью в координатах β-P, где траектории заметно расходятся, а газосодержание остается на уровне 5 – 30% (см. вставку на рис. 4). 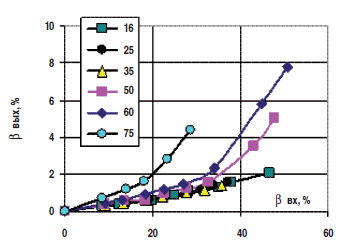 Рис. 4. Проекции траекторий 3D кривых Hст = fкр(β, P), построенных по данным исходных экспериментальных функций P = f(N), на плоскость β–P трехмерного пространства Hст–β–P. На увеличенном виде прямоугольником показана зона, использованная для обработки. Цифры на рисунке указывают Qж.нач. –βвх На влияние газа накладывается влияние других параметров, в частности сильное влияние величины Qж. Из данных экспериментов было сделано несколько выборок с близкими значениями Qж, а также более широкие выборки с большим разбросом величины Qж. Для расчетов использовали два вида экстраполяции данных: 1-я – с разбивкой кривых P – f(N) на три интервала ступеней и подбором экстраполирующих функций для каждого интервала отдельно (рис. 1а) и 2-я, когда использовалась только одна экстраполирующая функция для всей длины насоса. Результат во всех случаях обработки одинаковый – при росте β увеличивается наклон прямых, экстраполирующих зависимости напора ступени от давления.

Чтобы не увеличивать объем статьи, приводим результат только в одном из вариантов обработки в выборке с Qж = 55 – 59 м3/сут. (рис. 5). 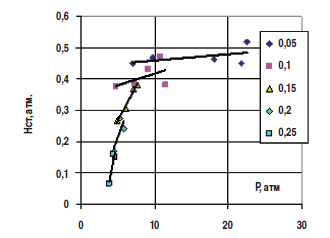 Рис. 5. Зависимости Hст – f(P) при заданных β по результатам обработки функций P – f(N) в выборке с Qж = 55 – 59 м3/сут. при экстраполяции функций P – f(N) тремя кривыми. Цифры на рисунках указывают на газосодержание На рис. 6 приведены данные об изменении наклона прямолинейных экстраполяций зависимостей Hст = f(P) на рис. 5, т. е. на зависимостях Hст от давления при заданных β (по выборке с Qж = 55 – 59 м3/сут.). 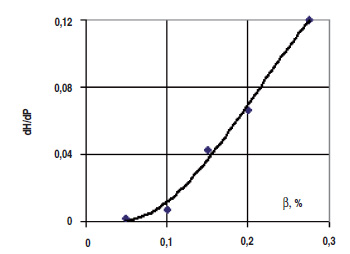 Рис. 6. Величина наклона прямых на зависимостях Hст = f(P) на рис. 5 от газосодержания в ГЖС – по выборке с Qж = 55–59 м3/сут. Таким образом, данные настоящей статьи подтверждают тот факт, что давление влияет на работу насоса или отдельной ступени на газожидкостной смеси [4, 15]. Обсуждение механизма такого влияния выходит за рамки настоящей статьи.

Обобщая полученные данные, в заключение можно представить вид функции Hст – f(β,P), которая постулировалась в [15] как некая характеристика единичной ступени в виде 3D поверхности в трехмерном пространстве Hст – P – β, рис. 7.

Это можно считать разве что первым (достаточно грубым) приближением, которое приводится здесь только в качестве наглядной иллюстрации представлений, развитых в [15] и в настоящей статье.

Для построения 3D траектории (на рис. 7а показано желтым), которая символизирует функцию Hст = fкр(β, P) для отдельного насоса при конкретных заданных Pвх и βвх, проведено сечение поверхности Hст-f(β,P) криволинейной цилиндрической поверхностью, проходящей через проекцию 3D кривой на плоскость β–P. Подобная проекция показана на рис. 2. 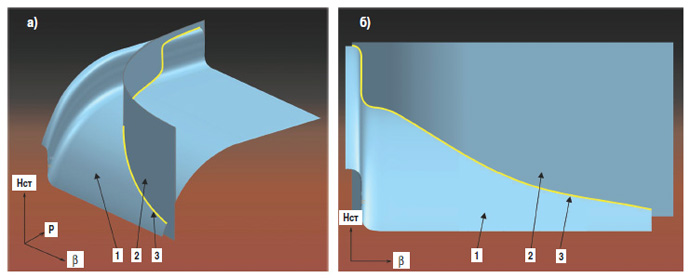 Рис. 7. Иллюстрации с помощью 3D построений: (а) – приблизительный вид поверхности Hст = f(β, P) и построение 3D траектории движения по поверхности Hст = f(β, P) по мере увеличения номера ступени, б – вид проекции 3D траектории на плоскость β–Hст (аналог рис. 1.г). 1 – характеристическая поверхность ступени Hст = f(β, P), 2 – поверхность, проходящая через 3D кривую Hст = f(β, P), построенная по проекции 3D кривой на плоскость β–P вытягиванием вдоль оси Hст, 3 – построение 3D кривой Hст = f(β, P) по пересечению поверхностей 1 и 2 Построения, рис. 7, в целом верно воспроизводят основные особенности экспериментальных результатов, полученных на длинной и коротких сборках.

Результаты настоящей статьи основаны на обработке данных экспериментов, которые не были проведены специально для выяснения влияния давления на входе. Они требуют перепроверки в экспериментах с более широким варьированием давления и газосодержания на входе с большим числом точек замера давления по длине насоса. И все же можно сделать следующие выводы: - Развитые в [15] и в настоящей статье представления позволяют проводить обработку данных по замерам распределения давления вдоль длины насосов и получать информацию о некой характеристике единичной ступени Hст = f(β, P). Каждое отдельное испытание дает возможность получить функцию отдельной траектории Hст = fкр(β,P) для заданных Pвх, βвх. Но из совокупности траекторий при соответствующем варьировании Pвх, βвх, возможно построение Hст = f(β, P).
- Сильное влияние давления касается сечений с заметным количеством газа в ГЖС при β = 0,3 – 0,25. Заметно влияние давления на сечениях β = 0,2 – 0,1, при β<0,1 превалирует влияние других факторов. Сильное влияние давления на работу ступеней в ГЖС, таким образом, проявляется только при больших газосодержаниях.
- Данные настоящей статьи подтверждают возможность работы обычных ступеней ВНН при высоких газосодержаниях на входе в ступень вплоть до β~65%. Постепенное снижение создаваемого единичной ступенью напора с увеличением β объясняется соответствующим снижением плотности ГЖС. Срыв работы насоса происходит из-за невыполнения условия:
∑1N Hn ≥ HC.
- Ляпков П.Д. Влияние газа на работу ступеней погружных центробежных насосов // Тр. ВНИИ. 1959. Вып. 22. С. 59 – 89.
- Дроздов А.Н. Технология и техника добычи нефти погружными насосами в осложненных условиях. М.: МАКС-пресс, 2008. 312 с.
- Игревский Л.В. Экспериментальные исследования влияния свободного газа на характеристики многоступенчатых погружных центробежных и центробежно-вихревых насосов // Надежность и сертификация оборудования для нефти и газа. 2002. № 3. С. 35 – 43.
- Дроздов А.Н. Влияние давления на образование каверны в потоке газожидкостной смеси за моделью лопасти центробежного насоса // Бурение и нефть. 2010. №2. С. 20 – 23.
- Дроздов А.Н. Закономерности работы многоступенчатого погружного центробежного насоса на газожидкостных смесях с низкой и высокой пенистостью // Территория – нефтегаз. 2009. № 6. С. 86 – 89.
- Дроздов А.Н., Сафиева Р.З., Филатов В.М. Пенистость нефти как важный фактор влияния свободного газа на характеристики погружного центробежного насоса // Территория – нефтегаз. 2008. № 6. С. 104 – 109.
- Дроздов А.Н., Сальманов Р.Г. Характеристики погружных лопастных насосов при откачке газожидкостных смесей // Территория – нефтегаз. 2009. №2. С. 36 – 40.
- Муравьев И.М., Мищенко И.Т. Эксплуатация погружных центробежных электронасосов в вязких жидкостях и газожидкостных смесях. М.: Недра., 1969. 248 с.
- Багманов А.А., Абуталипов Р.С. О работе центробежных насосов типа ЦНС на газонасыщенных водонефтяных эмульсиях // Тр. ин-та ВНИИСПТнефть.1988.Вып.II. С. 59 – 71.
- Рабочие характеристики ЭЦН с предвключенным диспергатором при работе на газожидкостной смеси / Пещеренко С.Н., Каплан А.Л., Ивашов А.А., Пещеренко М.П. // Бурение и нефть. 2011. №11.С. 42 – 44.
- Turpin J.L., Lea J.F. and Bearden J.L. / Gas-Liquid Flow Throuqh Cetrifuqal Pumps-Correlation of Data // Proc. 33rd Annual meeting of Southwestern petroleum short course, Lubbock, Texas 1986, pp 267 – 281.
- Гилев В.Г., Рабинович А.И. Особенности работы ступеней погружных насосов на смесях вода-воздух // Нефтепромысловое дело. 2006. №9. С. 40 – 48.
- Гилев В.Г., Рабинович А.И. Исследование распределения давлений в коротких сборках погружных насосов при работе на смесях «вода–воздух» // Нефтепромысловое дело. 2008. №.6. С. 56 – 62.
- Гилев В.Г., Рабинович А.И. Агеев Ш.Р. Методика оценки параметров многоступенчатых погружных насосов на единичной ступени // Нефтепромысловое дело. 2009. № 2. С. 36 – 41.
- Гилев В.Г., Рабинович А.И., Кобяков А.Е. К вопросу о расчете и методе испытаний насосов на ГЖС. Метод расчета и требования к методике получения характеристики единичной ступени // Бурение и нефть. 2012. №2. С. 38 – 42.
- Visualization study of performance breakdown in two-phase performance of an electrical submersible pump / Gamboa J., Prado M.G. // Proceedings of the 26th International Pump User Symposium (2010) http://turbolab.tamu.edu/uploads/files/papers/p26/ch01_Gamboa.pdf
- P.D. Lyapkov. Gas influence on work of stages of submersible centrifugal pumps // VNII works. 1959, Issue # 22. Pp. 59-89.
- A.N. Drozdov. Technology & technics of oil production by submersible pumps in complicated conditions. M.: MAKS press. 2008. 312 pages.
- L.V. Igrevsky. Experimental surveys of free gas influence on characteristics of multistage submersible centrifugal & centrifugal-vortex pumps // Reliability & certification of equipment for oil & gas. 2002. #3. Pp. 35-43.
- A.N. Drozdov. Pressure influence on cavern forming in flow of gas-liquid mixture behind blade model of centrifugal pump // Burenie i neft. 2010. #2. Pp. 20-23.
- A.N. Drozdov. Work regularities of multistage submersible centrifugal pump with gas-liquid mixtures (low & high foaminess) // Territory oil & gas. 2009. #6. Pp. 86-89.
- A.N. Drozdov, R.Z. Safieva, V.M. Filatov. Oil foaminess as important factor of free gas influence on characteristics of submersible centrifugal pump // Territory oil & gas. 2008. #6. Pp. 104-109.
- A.N. Drozdov, R.G. Sal’manov. Characteristics of submersible blade pumps when pumping-out of gas-liquid mixtures // Territory oil & gas. 2009. #2. Pp. 36-40.
- I.M. Murav’yov, I.T. Mishchenko. Exploitation of submersible centrifugal electric pumps in viscous liquids & gas-liquid mixtures. M.: Bowels. 1969. 248 pages.
- A.A. Bagmanov, R.S. Abutalipov. About work of CNS-type centrifugal pumps with gas-saturated water-oil emulsions // VNIISPTneft institute’s works. 1988, issue II. Pp. 59-71.
- Working characteristics of electric centrifugal pumps with pre-switched dispersant working with gas-liquid mixture / S.N. Peshcherenko, A.L. Kaplan, A.A. Ivashov, M.P. Peshcherenko // Burenie i neft. 2011. #11. Pp. 42-44.
- Turpin J.L., Lea J.F. and Bearden J.L. / Gas-Liquid Flow Through Cetrifugal Pumps-Correlation of Data // Proc. 33rd Annual meeting of Southwestern petroleum short course, Lubbock, Texas 1986, pp. 267 - 281.
- V.G. Gilev, A.I. Rabinovich. Work peculiarities of submersible pumps’ stages with water-air mixtures // Oil field business. 2006. #9. Pp. 40-48.
- V.G. Gilev, A.I. Rabinovich. Survey of pressures’ distribution in short assemblies of submersible pumps when working with water-air mixtures // Oil field business. 2008. #6. Pp. 56-62.
- V.G. Gilev, A.I. Rabinovich, Sh.R. Ageev. Parameters’ assessment methods of multistage submersible pumps at single stage // Oil field business. 2009. #2. Pp. 36-41.
- V.G. Gilev, A.I. Rabinovich, A.Ye. Kobyakov. On calculation & method of pumps’ tests with gas-liquid mixtures. Computing methods & requirements to obtaining methods of single stage’s characteristic // Burenie i neft. 2012. #2. Pp. 38-42.
- Visualization study of performance breakdown in two-phase performance of an electrical submersible pump / Gamboa J., Prado M.G. // Proceedings of the 26th International Pump User Symposium (2010) http://turbolab.tamu.edu/uploads/files/papers/p26/ch01_Gamboa.pdf
Комментарии посетителей сайта
| 

Гилев В.Г.
к.т.н., инженер-исследователь инженерно-технического центра
ЗАО «Новомет-Пермь»

Рабинович А.И.
советник генерального директора по новой технике
ЗАО «Новомет-Пермь»
Ивашов А.А.
инженер-исследователь инженерно-технического центра
ЗАО «Новомет-Пермь»

Агеев Ш.Р.
заведующий отделом прикладной гидродинамики
ОАО «ОКБ БН Коннас»
Ключевые слова: многоступенчатый погружной центробежный насос, газожидкостная смесь Keywords: multistage submersible centrifugal pump, gas-liquid mixture
Просмотров статьи: 4646
|












